The following is from Unraveled: An Evidence-Based Approach to Understanding and Preventing Crime
Amazon (Paperback) Amazon (Kindle) Apple Barnes & Noble Google
Emile Durkheim, a pioneer in criminology, suggested that crime was not indicative of a pathology or illness in society but at certain levels, crime was simply evidence of the normal functioning of communities. A normal level of crime, referred to as endemic crime, helps to define and solidify norms in society. Data analyzed by criminologist David Weisburd and his colleagues confirmed that there is indeed a “normal level of crime” in cities. They expanded on Durkheim’s proposition in stating that the normal level of crime relates to the concentration of crime at a place rather than to an overall rate of crime.[i]
Organizations can identify normal (endemic) threat levels at their properties (places) by identifying those places that fall outside the norm. A simple method for determining which places are high crime is to identify those at the top 10 percent of places, among a set of comparable places, that account for the majority of the crime.[ii] A more sophisticated and objective method for identifying normal levels of crime is by calculating crime thresholds.[iii] A crime threshold analysis is used to statistically determine the normal range of crime for a place relative to other places. Security decision makers “need to know the upper and lower limits (known as thresholds) of each crime in order to determine if they are either within, above, or below their expected levels.”[iv] Crime thresholds provide an “objective basis for determining when crime is getting out of hand.”[v] For organizations with large numbers of similar properties, this is easier.
A threshold analysis is most useful when comparing similar places. While “similar” can be a subjective term when applied to places, organizations that operate one type of business will likely find similarity among their businesses. For example, a grocery chain that serves a specific, defined population (e.g., Whole Foods) may consider all their stores to be similar. Alternatively, the organization may consider only their grocery stores in one geographic area to be similar (e.g., Whole Foods stores in Austin, Texas). Regardless of the method employed to group places by similarity, the formulas for calculating the threshold remain the same.
Threshold analysis is best explained by way of illustration. The following table is for a retail chain with ten stores. All ten stores are located within the metropolitan area of a large urban city. During a three-year period, the stores experience a range of thefts.
| Store Number | Thefts |
| Store 01 | 137 |
| Store 02 | 82 |
| Store 03 | 70 |
| Store 04 | 49 |
| Store 05 | 13 |
| Store 06 | 199 |
| Store 07 | 116 |
| Store 08 | 74 |
| Store 09 | 56 |
| Store 10 | 42 |
For this dataset, the average (mean) number of thefts among these stores is calculated at 83.8. With the average number of thefts determined, the high and low thresholds of the dataset need to be calculated. The high threshold is the upper limit of normal crime for the dataset, while a low threshold is the lower level for the dataset. Thresholds are calculated using standard deviation:[vi]
Other researchers have defined high risk places as those that exceed two standard deviations from the mean.[vii] Standard deviation is a measure of the dispersion of a frequency distribution that is the square root of the arithmetic mean of the squares of the deviation of each of the class frequencies from the arithmetic mean of the frequency distribution.[viii] Standard deviation discloses how the values are spread out from the mean. A low standard deviation means that most of the numbers are close to the mean. A high standard deviation means that the numbers are more spread out from the mean.
The standard deviation is a measure of the normal distribution of the dataset. A normal distribution in the theft example means that most of the stores have thefts that are close to average, while fewer stores tend to be outside the normal range. Statistically, 68 percent of all crimes will occur within one standard deviation, 95 percent will occur within two standard deviations, and 99.7 percent between three standard deviations. A crime level within one standard deviation could be considered normal or endemic crime.[ix] While standard deviation could be considered an arbitrary indicator, when applied uniformly across similar facilities, it provides a good baseline for comparison. Other indicators may be used as dictated by the needs of the analysis. For example, the analyst could arbitrarily assign two standard deviations above mean as a high crime threshold.
The standard deviation is 51.2 in the theft dataset. Using the formulas above, a high threshold of 135.0 and a low threshold of 32.6 can be calculated. This information is illustrated graphically below.
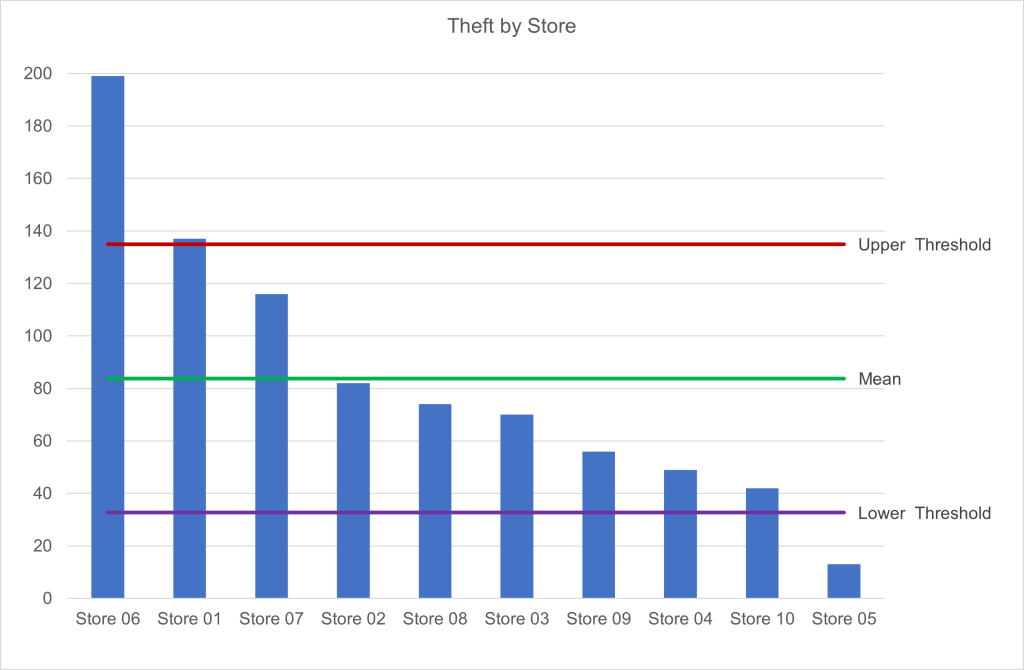
In this example, the columns represent the total number of thefts at each store during the past three years. The middle horizontal line represents the average number of thefts (mean) among these stores. The top horizontal line represents the high threshold (mean + one standard deviation). The bottom horizontal line represents the low threshold (mean + one standard deviation). Relative to the other stores in the dataset, Store 06, Store 01, and Store 05 are outside the range of “normal” crime. The number of thefts at Stores 07, 02, 08, 03, 09, 04, and 10 falls within the low and high thresholds. As such, they exhibit a normal level of theft relative to the other stores in the dataset.
The higher concentration of theft at Store 06 and Store 01, as shown on the left side of the graph, is referred to as power law, Pareto Principle, or more commonly, the 80/20 rule.[x] Applying appropriate security measures to these stores will likely yield the most benefit. As discussed in Chapter 2, criminological research has found similar distributions across various data sets, including 20.3 percent of stores experiencing 84.9 percent of shopliftings and 19 percent of motels contributing to 51.1 percent of calls for police service.[xi]
Crime thresholds are used by some municipalities and other government entities to identify places requiring government intervention, such as application of nuisance abatement laws or other similar enforcement actions. The Houston Police Department’s Apartment Enforcement Unit, for example, calculates crime thresholds at all apartment complexes in the city using the same methodology described in this section. The Houston Police Department method was developed in collaboration with the Department of Criminal Justice and Criminology at Sam Houston State University. To compensate for the variety of apartment sizes, the Apartment Enforcement Unit adjusts their thresholds using occupancy rates at each apartment property. The Apartment Enforcement Unit calculates three different thresholds using the apartment crime data:
- UCR Part 1 Crime
- UCR Part 2 Crime
- Nuisance Crimes (as defined by Texas law)
Apartment properties that exceed the nuisance crime threshold are then subjected to an intervention by the Houston Police Department, which seeks voluntary compliance from place managers to implement crime prevention initiatives. If nuisance crimes do not fall back into the normal (endemic) range or if the place manager fails to comply with the police department’s suggestions, the city may seek involuntary compliance via a nuisance abatement lawsuit.
[i] Weisburd, D., Groff, E., & Yang, S-M. (2012), The criminology of place: Street segments and our understanding of the crime problem. Oxford University Press.
[ii] Eck, J. E. (2017). Opportunity structure for bad place management: A theory to assist effective regulation of high crime places. In D. S. Weisburd & J. E. Eck (Eds.), Unraveling the crime-place connection: New directions in theory and policy (vol. 22). Routledge.
[iii] Woods, M. (1999). Crime analysis: A key tool in any crime reduction strategy. Police Chief, 66(4).
[iv] Gottlieb, S. (1994). Crime analysis: From first report to final arrest. Alpha Publishing.
[v] Gottlieb, S. (1994). Crime analysis: From first report to final arrest. Alpha Publishing.
[vi] The use of one standard deviation is a normative decision, not a scientific one. Some organizations use 0.5, 1.5, or 2 standard deviations.
[vii] Caplan, J. M., Kennedy, L. W., Drawve, G., & Baughman, J. H. (2021). Data-informed and place-based violent crime prevention: The Kansas City, Missouri risk-based policing initiative. Police Quarterly. https://doi.org/10.1177/10986111211003205
[viii] https://www.merriam-webster.com/dictionary/standard%20deviation
[ix] Gottlieb, S. (1994). Crime analysis: From first report to final arrest. Alpha Publishing.
[x] Eck, J. E., Clarke, R. V., & Guerette, R. T. (2007). Risky facilities: Crime concentration in homogeneous sets of establishments and facilities. In G. Farrell, K. J. Bowers, S. D. Johnson, & M. Townsley (Eds.), Imagination for crime prevention, Crime prevention studies (vol. 21). Criminal Justice Press.
[xi] Eck, J. E., Clarke, R. V., & Guerette, R. T. (2007). Risky facilities: Crime concentration in homogeneous sets of establishments and facilities. In G. Farrell, K. J. Bowers, S. D. Johnson, & M. Townsley (Eds.), Imagination for crime prevention, Crime prevention studies (vol. 21). Criminal Justice Press.